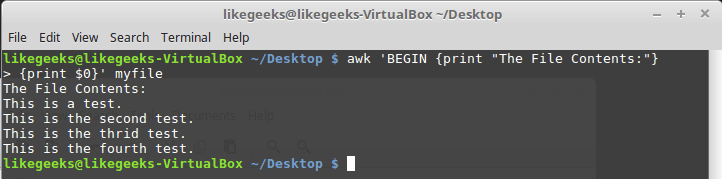
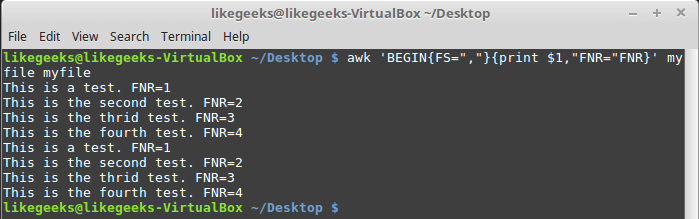
Looking up for entries that satisfy a specific condition is a painful process, especially if you are searching it in a large dataset having hundreds or thousands of entries. If you know the fundamental SQL queries, you must be aware of the ‘WHERE’ clause that is used with the SELECT statement to fetch such entries from a relational database that satisfy certain conditions. NumPy offers similar functionality to find such items in a NumPy array that satisfy a given Boolean condition through its ‘where()‘ function — except that it is used in a slightly different way than the SQL SELECT statement with the WHERE clause. In this tutorial, we’ll look at the various ways the NumPy where function can be used for a variety of use cases. Let’s get going.
Looking up for entries that satisfy a specific condition is a painful process, especially if you are searching it in a large dataset having hundreds or thousands of entries. If you know the fundamental SQL queries, you must be aware of the ‘WHERE’ clause that is used with the SELECT statement to fetch such entries from a relational database that satisfy certain conditions. NumPy offers similar functionality to find such items in a NumPy array that satisfy a given Boolean condition through its ‘where()‘ function — except that it is used in a slightly different way than the SQL SELECT statement with the WHERE clause. In this tutorial, we’ll look at the various ways the NumPy where function can be used for a variety of use cases. Let’s get going.
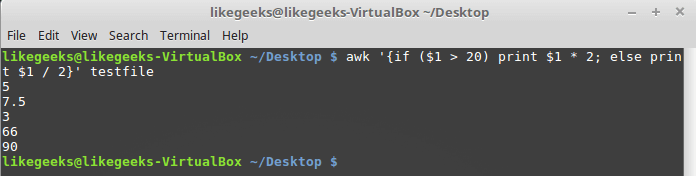
A very simple usage of NumPy where
Let’s begin with a simple application of ‘np.where()‘ on a 1-dimensional NumPy array of integers.
We will use ‘np.where’ function to find positions with values that are less than 5.
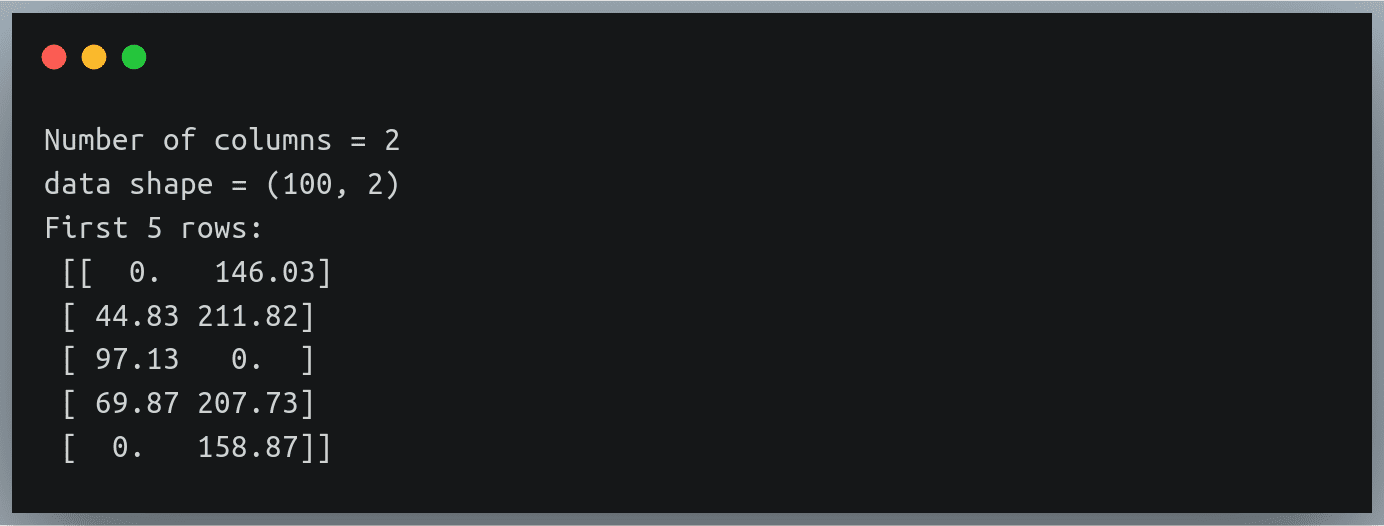
We’ll first create a 1-dimensional array of 10 integer values randomly chosen between 0 and 9.
import numpy as np
np.random.seed(42)
a = np.random.randint()
print("a = {}".format(a))
Output:
a = [6 3 7 4 6 9 2 6 7 4]
Now we will call ‘np.where’ with the condition ‘a < 5’ i.e we’re asking ‘np.where’ to tell us where in the array a are the values less than 5. It will return us an array of indices where the specified condition is satisfied.
result = np.where(a < 5)
print(result)
Output:
(array([1, 3, 6, 9]),)
We get the indices 1,3,6,9 as output and it can be verified from the array that the values at these positions are indeed less than 5.
Note that the returned value is a 1-element tuple. This tuple has an array of indices.
We’ll understand the reason for the result being returned as a tuple when we discuss np.where on 2D arrays.
How does NumPy where work?
To understand what goes on inside the complex expression involving the ‘np.where’ function, it is important to understand the first parameter of ‘np.where’, that is, the condition.
When we call a Boolean expression involving NumPy array such as ‘a > 2’ or ‘a % 2 == 0’, it actually returns a NumPy array of Boolean values.
This array has the value True at positions where the condition evaluates to True and has the value False elsewhere. This serves as a ‘mask‘ for NumPy where function.
Here is a code example.
a = np.array([1, 10, 13, 8, 7, 9, 6, 3, 0])
print ("a > 5:")
print(a > 5)
Output:
a > 5:
[false True True True True True True False False]
So what we effectively do is that we pass an array of Boolean values to the ‘np.where’ function which then returns the indices where the array had the value True.
This can be verified by passing a constant array of Boolean values instead of specifying the condition on the array that we usually do.
bool_array = np.array([True, True, True, False, False, False, False, False, False])
print(np.where(bool_array)
Output:
(array([0, 1, 2]),)
Notice how, instead of passing a condition on an array of actual values, we passed a Boolean array and the ‘np.where’ function returned us the indices where the values were True.
2D matrices
Now that we have seen it on 1-dimensional NumPy arrays, let us understand how would ‘np.where’ behave on 2D matrices.
The idea remains the same. We call the ‘np.where’ function and pass a condition on a 2D matrix. The difference is in the way it returns the result indices.
Earlier, np.where returned a 1-dimensional array of indices (stored inside a tuple) for a 1-D array, specifying the positions where the values satisfy a given condition.
But in the case of a 2D matrix, a single position is specified using 2 values — the row index and the column index.
So in this case, np.where will return 2 arrays, the first one carrying the row indices and the second one carrying the corresponding column indices.
Both these rows and column index arrays are stored inside a tuple (now you know why we got a tuple as an answer even in case of a 1-D array).
Let’s see this in action to better understand it.
We’ll write a code to find where in a 3×3 matrix are the entries divisible by 2.
np.random.seed(42)
a = np.random.randint(0,10, size=(3,3))
print("a =\n{}\n".format(a))
result = np.where(a % 2 == 0)
print("result: {}".format(result))
Output:
a =
[[6 3 7]
[4 6 9]
[2 6 7]
result: (array([0, 1, 1, 2, 2]], array([0, 0, 1, 0, 1]))
The returned tuple has 2 arrays, each bearing the row and column indices of the positions in the matrix where the values are divisible by 2.
Ordered pairwise selection of values from the two arrays gives us a position each.
The length of each of the two arrays is 5, indicating there are 5 such positions satisfying the given condition.
If we look at the 3rd pair — (1,1), the value at (1,1) in the matrix is 6 which is divisible by 2.
Likewise, you can check and verify with other pairs of indices as well.
Multidimensional array
Just as we saw the working of ‘np.where’ on a 2-D matrix, we will get similar results when we apply np.where on a multidimensional NumPy array.
The length of the returned tuple will be equal to the number of dimensions of the input array.
Each array at position k in the returned tuple will represent the indices in the kth dimension of the elements satisfying the specified condition.
Let’s quickly look at an example.
np.random.seed(42)
a = np.random.randint(0,10, size=(3,3,3,3)) #4-dimensional array
print("a =\n{}\n".format(a))
result = np.where(a == 5) #checking which values are equal to 5
print("len(result)= {}".format(len(result)))
print("len(result[0]= {})".format(len(result[0])))
Output:
len(result) = 4 indicates the input array is of 4 dimension.
The length of one of the arrays in the result tuple is 6, which means there are six positions in the given 3x3x3x3 array where the given condition (i.e containing value 5) is satisfied.
Using the result as an index
So far we have looked at how we get the tuple of indices, in each dimension, of the values satisfying the given condition.
Most of the time we’d be interested in fetching the actual values satisfying the given condition instead of their indices.
To achieve this, we can use the returned tuple as an index on the given array. This will return only those values whose indices are stored in the tuple.
Let’s check this for the 2-D matrix example.
np.random.seed(42)
a = np.random.randint(0,10, size=(3,3))
print("a =\n{}\n".format(a))
result_indices = np.where(a % 2 == 0)
result = a[result_indices]
print("result: {}".format(result))
Output:
a =
[[6 3 7]
[4 6 9]
[2 6 7]]
result: [6 4 6 2 6]
As discussed above, we get all those values (not their indices) that satisfy the given condition which, in our case, was divisibility by 2 i.e even numbers.
Parameters ‘x’ and ‘y’
Instead of getting the indices as a result of calling the ‘np.where’ function, we can also provide as parameters, two optional arrays x and y of the same shape (or broadcastable shape) as input array, whose values will be returned when the specified condition on the corresponding values in input array is True or False respectively.
For instance, if we call the method on a 1-dimensional array of length 10, and we supply two more arrays x and y of the same length.
In this case, whenever a value in input array satisfies the given condition, the corresponding value in array x will be returned whereas, if the condition is false on a given value, the corresponding value from array y will be returned.
These values from x and y at their respective positions will be returned as an array of the same shape as the input array.
Let’s get a better understanding of this through code.
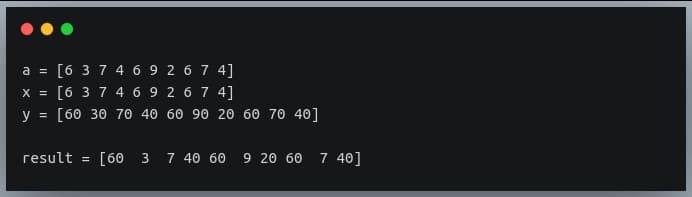
np.random.seed(42)
a = np.random.randint(0,10, size=(10))
x = a
y = a*10
print("a = {}".format(a))
print("x = {}".format(x))
print("y = {}".format(y))
result = np.where(a%2 == 1, x, y) #if number is odd return the same number else return its multiple of 10.
print("\nresult = {}".format(result))
Output:
This method is useful if you want to replace the values satisfying a particular condition by another set of values and leaving those not satisfying the condition unchanged.
In that case, we will pass the replacement value(s) to the parameter x and the original array to the parameter y.
Note that we can pass either both x and y together or none of them. We can’t pass one of them and skip the other.
Apply on Pandas DataFrames
Numpy’s ‘where’ function doesn’t necessarily have to be applied to NumPy arrays. It can be used with any iterable that would yield a list of Boolean values.
Let us see how we can apply the ‘np.where’ function on a Pandas DataFrame to see if the strings in a column contain a particular substring.
import pandas as pd
import numpy as np
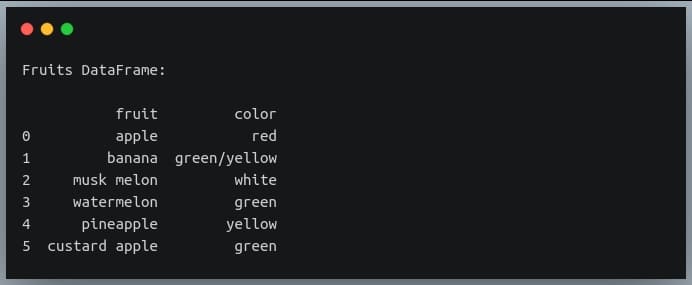
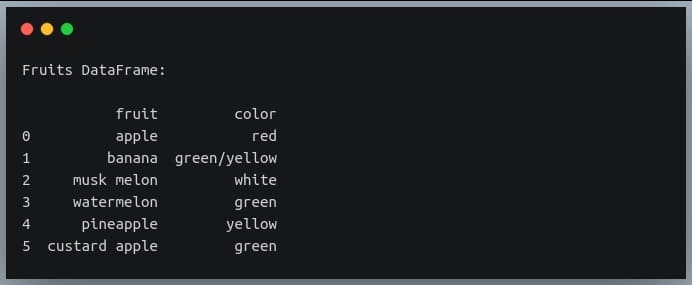
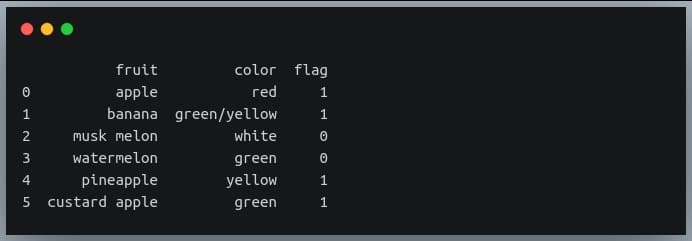
df = pd.DataFrame({"fruit":["apple", "banana", "musk melon",
"watermelon", "pineapple", "custard apple"],
"color": ["red", "green/yellow", "white",
"green", "yellow", "green"]})
print("Fruits DataFrame:\n")
print(df)
Output:
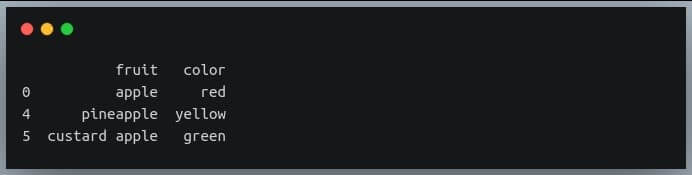
Now we’re going to use ‘np.where’ to extract those rows from the DataFrame ‘df’ where the ‘fruit’ column has the substring ‘apple’
apple_df = df.iloc[np.where(df.fruit.str.contains("apple"))]
print(apple_df)
Output:
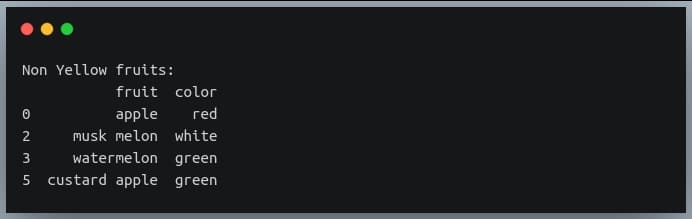
Let’s try one more example on the same DataFrame where we extract rows for which the ‘color’ column does not contain the substring ‘yell’.
Note: we use the tilde (~) sign to inverse Boolean values in Pandas DataFrame or a NumPy array.
non_yellow_fruits = df.iloc[np.where(~df.color.str.contains("yell"))]
print("Non Yellow fruits:\n{}".format(non_yellow_fruits))
Output:
Multiple conditions
So far we have been evaluating a single Boolean condition in the ‘np.where’ function. We may sometimes need to combine multiple Boolean conditions using Boolean operators like ‘AND‘ or ‘OR’.
It is easy to specify multiple conditions and combine them using a Boolean operator.
The only caveat is that for the NumPy array of Boolean values, we cannot use the normal keywords ‘and’ or ‘or’ that we typically use for single values.
We need to use the ‘&’ operator for ‘AND’ and ‘|’ operator for ‘OR’ operation for element-wise Boolean combination operations.
Let us understand this through an example.
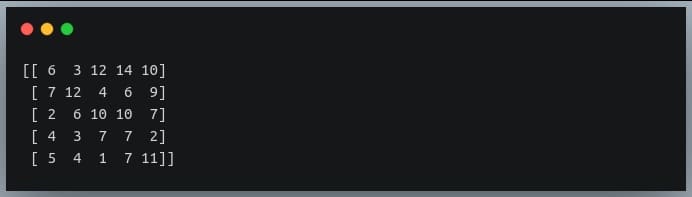
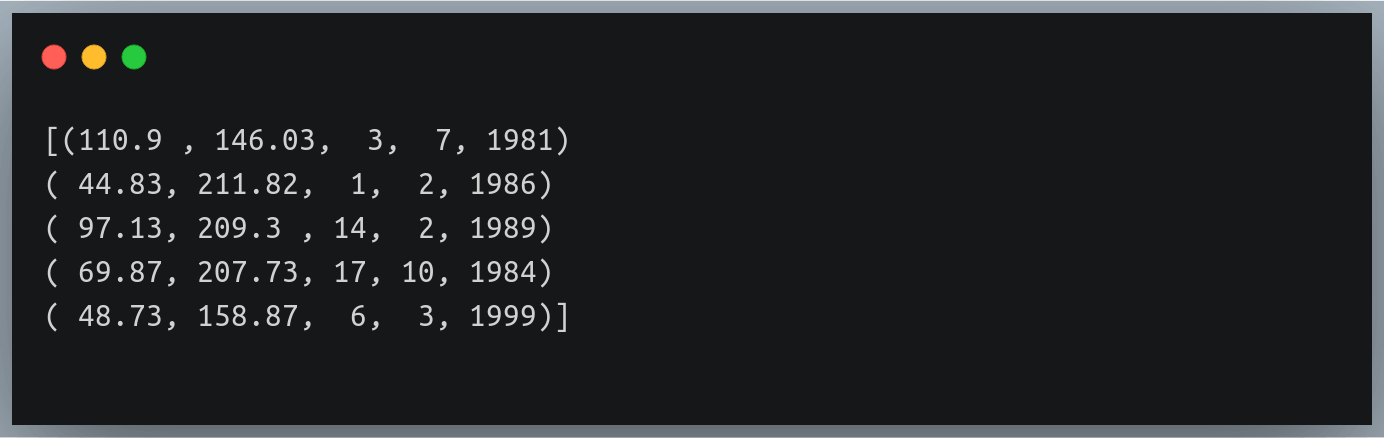
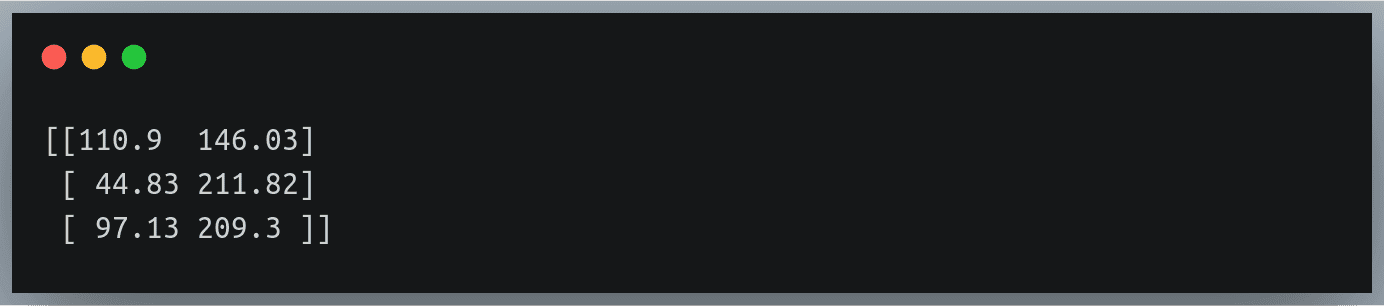
np.random.seed(42)
a = np.random.randint(0,15, (5,5)) #5x5 matrix with values from 0 to 14
print(a)
Output:
We will look for values that are smaller than 8 and are odd. We can combine these two conditions using the AND (&) operator.
# get indices of odd values less than 8 in a
indices = np.where((a < 8) & (a % 2==1))
#print the actual values
print(a[indices])
Output:
We can also use the OR (|) operator to combine the same conditions. This will give us values that are ‘less than 8’ OR ‘odd values’ i.e all values less than 8 and all odd values greater than 8 will be returned.
# get indices of values less than 8 OR odd values in a
indices = np.where((a < 8) | (a % 2==1))
#print the actual values
print(a[indices])
Output:
Nested where (where within where)
Let us revisit the example of our ‘fruits’ table.
import pandas as pd
import numpy as np
df = pd.DataFrame({"fruit":["apple", "banana", "musk melon",
"watermelon", "pineapple", "custard apple"],
"color": ["red", "green/yellow", "white",
"green", "yellow", "green"]})
print("Fruits DataFrame:\n")
print(df)
Output:
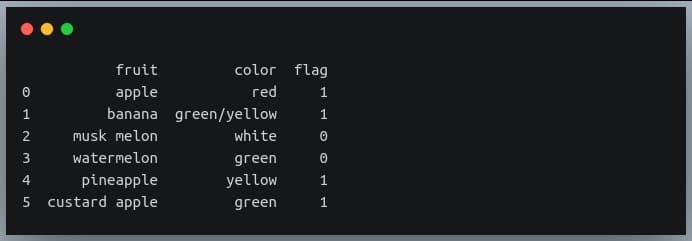
Now let us suppose we wanted to create one more column ‘flag’ which would have the value 1 if the fruit in that row has a substring ‘apple’ or is of color ‘yellow’. We can achieve this by using nested where calls i.e we will call ‘np.where’ function as a parameter within another ‘np.where’ call.
df['flag'] = np.where(df.fruit.str.contains("apple"), 1, # if fruit == 'apple', set 1
np.where(df.color.str.contains("yellow"), 1, 0)) #else if color has 'yellow' set 1, else set 0
print(df)
Output:
The complex expression above can be translated into simple English as:
- If the ‘fruit’ column has the substring ‘apple’, set the ‘flag’ value to 1
- Else:
- If the ‘color’ column has substring ‘yellow’, set the ‘flag’ value to 1
- Else set the ‘flag’ value to 0
Note that we can achieve the same result using the OR (|) operator.
#set flag = 1 if any of the two conditions is true, else set it to 0
df['flag'] = np.where(df.fruit.str.contains("apple") |
df.color.str.contains("yellow"), 1, 0)
print(df)
Output:
Thus nested where is particularly useful for tabular data like Pandas DataFrames and is a good equivalent of the nested WHERE clause used in SQL queries.
Finding rows of zeros
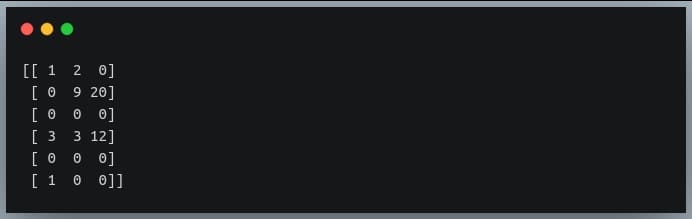
Sometimes, in a 2D matrix, some or all of the rows have all values equal to zero. For instance, check out the following NumPy array.
a = np.array([[1, 2, 0],
[0, 9, 20],
[0, 0, 0],
[3, 3, 12],
[0, 0, 0]
[1, 0, 0]])
print(a)
Output:
As we can see the rows 2 and 4 have all values equal to zero. But how do we find this using the ‘np.where’ function?
If we want to find such rows using NumPy where function, we will need to come up with a Boolean array indicating which rows have all values equal to zero.
We can use the ‘np.any()‘ function with ‘axis = 1’, which returns True if at least one of the values in a row is non-zero.
The result of np.any() will be a Boolean array of length equal to the number of rows in our NumPy matrix, in which the positions with the value True indicate the corresponding row has at least one non-zero value.
But we needed a Boolean array that was quite the opposite of this!
That is, we needed a Boolean array where the value ‘True’ would indicate that every element in that row is equal to zero.
Well, this can be obtained through a simple inversion step. The NOT or tilde (~) operator inverts each of the Boolean values in a NumPy array.
The inverted Boolean array can then be passed to the ‘np.where’ function.
Ok, that was a long, tiring explanation.
Let’s see this thing in action.
zero_rows = np.where(~np.any(a, axis=1))[0]
print(zero_rows)
Output:
Let’s look at what’s happening step-by-step:
- np.any() returns True if at least one element in the matrix is True (non-zero).
axis = 1indicates it to do this operation row-wise. - It would return a Boolean array of length equal to the number of rows in a, with the value True for rows having non-zero values, and False for rows having all values = 0.
np.any(a, axis=1)
Output:
3.The tilde (~) operator inverts the above Boolean array:
~np.any(a, axis=1)
Output:
- ‘np.where()’ accepts this Boolean array and returns indices having the value True.
The indexing [0] is used because, as discussed earlier, ‘np.where’ returns a tuple.
Finding the last occurrence of a true condition
We know that NumPy’s ‘where’ function returns multiple indices or pairs of indices (in case of a 2D matrix) for which the specified condition is true.
But sometimes we are interested in only the first occurrence or the last occurrence of the value for which the specified condition is met.
Let’s take the simple example of a one-dimensional array where we will find the last occurrence of a value divisible by 3.
np.random.seed(42)
a = np.random.randint(0,10, size=(10))
print("Array a:", a)
indices = np.where(a%3==0)[0]
last_occurrence_position = indices[-1]
print("last occurrence at", last_occurrence_position)
Output:
Here we could directly use the index ‘-1’ on the returned indices to get the last value in the array.
But how would we extract the position of the last occurrence in a multidimensional array, where the returned result is a tuple of arrays and each array stores the indices in one of the dimensions?
We can use the zip function which takes multiple iterables and returns a pairwise combination of values from each iterable in the given order.
It returns an iterator object, and so we need to convert the returned object into a list or a tuple or any iterable.
Let’s first see how zip works:
a = (1, 2, 3, 4)
b = (5, 6, 7, 8)
c = list(zip(a,b))
print(c)
Output:
So the first element of a and the first element of b form a tuple, then the second element of a and the second element of b form the second tuple in c, and so on.
We’ll use the same technique to find the position of the last occurrence of a condition being satisfied in a multidimensional array.
Let’s use it for a 2D matrix with the same condition as we saw in the earlier example.
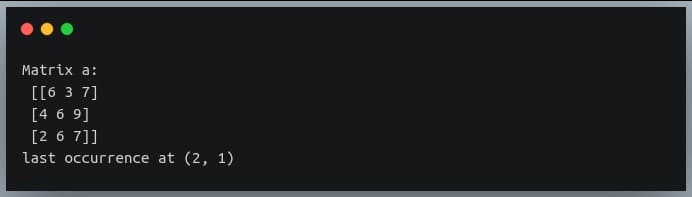
np.random.seed(42)
a = np.random.randint(0,10, size=(3,3))
print("Matrix a:\n", a)
indices = np.where(a % 3 == 0)
last_occurrence_position = list(zip(*indices))[-1]
print("last occurrence at",last_occurrence_position)
Output:
We can see in the matrix the last occurrence of a multiple of 3 is at the position (2,1), which is the value 6.
Note: The * operator is an unpacking operator that is used to unpack a sequence of values into separate positional arguments.
Using on DateTime data
We have been using ‘np.where’ function to evaluate certain conditions on either numeric values (greater than, less than, equal to, etc.), or string data (contains, does not contain, etc.)
We can also use the ‘np.where’ function on datetime data.
For example, we can check in a list of datetime values, which of the datetime instances are before/after a given specified datetime.
Let’s understand this through an example.
Note: We’ll use Python’s datetime module to create date objects.
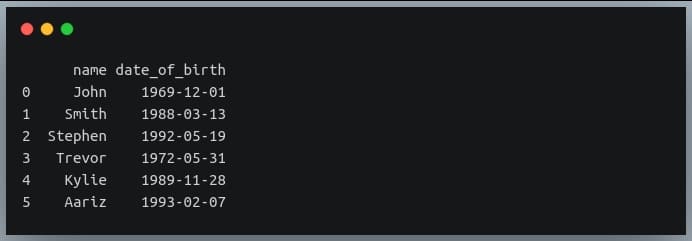
Let’s first define a DataFrame specifying the dates of birth of 6 individuals.
import datetime
names = ["John", "Smith", "Stephen", "Trevor", "Kylie", "Aariz"]
dob = [datetime.datetime(1969, 12, 1),
datetime.datetime(1988, 3, 13),
datetime.datetime(1992, 5, 19),
datetime.datetime(1972, 5, 31),
datetime.datetime(1989, 11, 28),
datetime.datetime(1993, 2, 7)]
data_birth = pd.DataFrame({"name":names, "date_of_birth":dob})
print(data_birth)
Output:
This table has people from diverse age groups!
Let us now specify a condition where we are interested in those individuals who are born on or post-January 1, 1990.
post_90_indices = np.where(data_birth.date_of_birth >= '1990-01-01')[0]
print(post_90_indices)
Output:
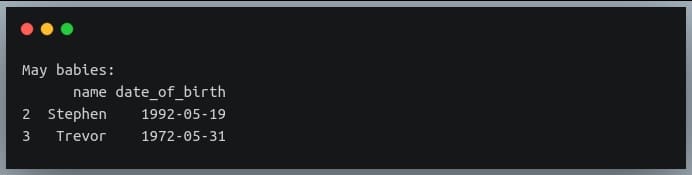
Rows 2 and 5 have Smith and Kylie who are born in the years 1992 and 1993 respectively.
Here we are using the ‘greater than or equal to’ (>=) operator on a datetime data, which we generally use with numeric data.
This is possible through operator overloading.
Let’s try one more example. Let’s fetch individuals that were born in May.
Note: Pandas Series provides ‘dt’ sub-module for datetime specific operations, similar to the ‘str’ sub-module we saw in our earlier examples.
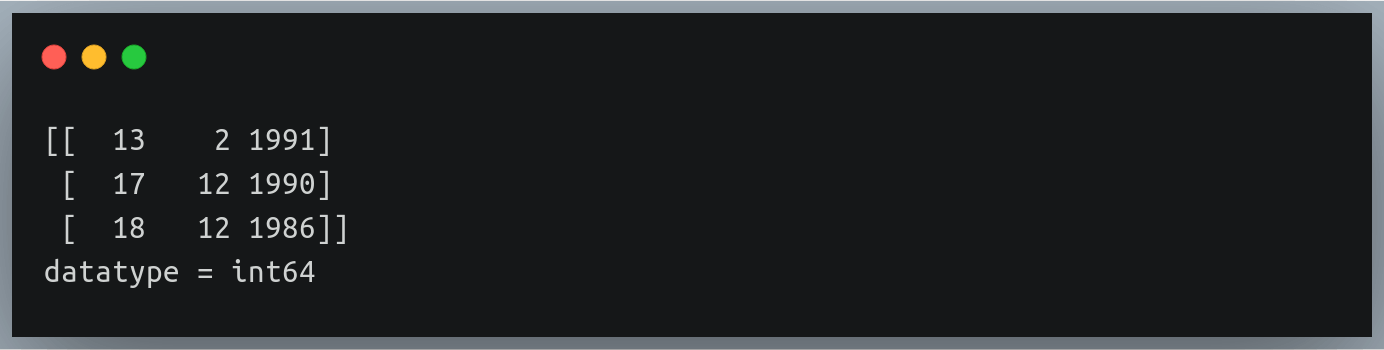
may_babies = data_birth.iloc[np.where(data_birth.date_of_birth.dt.month == 5)]
print("May babies:\n{}".format(may_babies))
Output:
Conclusion
We began the tutorial with simple usage of ‘np.where’ function on a 1-dimensional array with conditions specified on numeric data.
We then looked at the application of ‘np.where’ on a 2D matrix and then on a general multidimensional NumPy array.
We also understood how to interpret the tuple of arrays returned by ‘np.where’ in such cases.
We then understood the functionality of ‘np.where’ in detail, using Boolean masks.
We also saw how we can use the result of this method as an index to extract the actual original values that satisfy the given condition.
We looked at the behavior of the ‘np.where’ function with the optional arguments ‘x’ and ‘y’.
We then checked the application of ‘np.where’ on a Pandas DataFrame, followed by using it to evaluate multiple conditions.
We also looked at the nested use of ‘np.where’, its usage in finding the zero rows in a 2D matrix, and then finding the last occurrence of the value satisfying the condition specified by ‘np.where’
Finally, we used ‘np.where’ function on a datetime data, by specifying chronological conditions on a datetime column in a Pandas DataFrame.












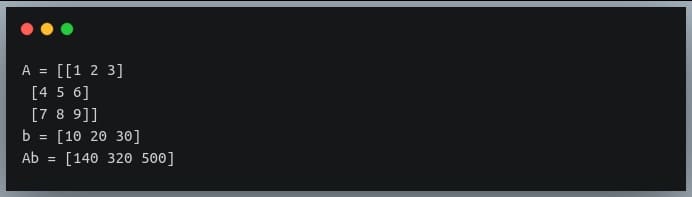
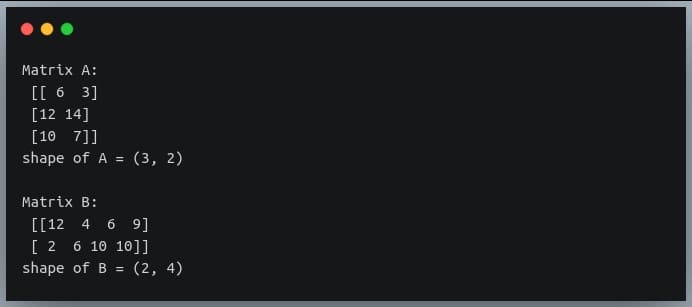
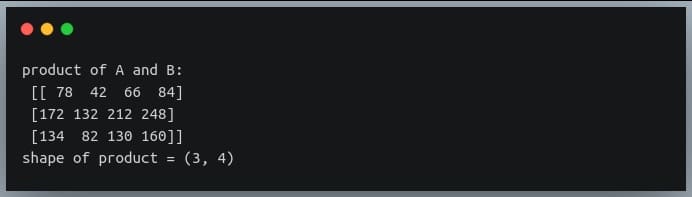
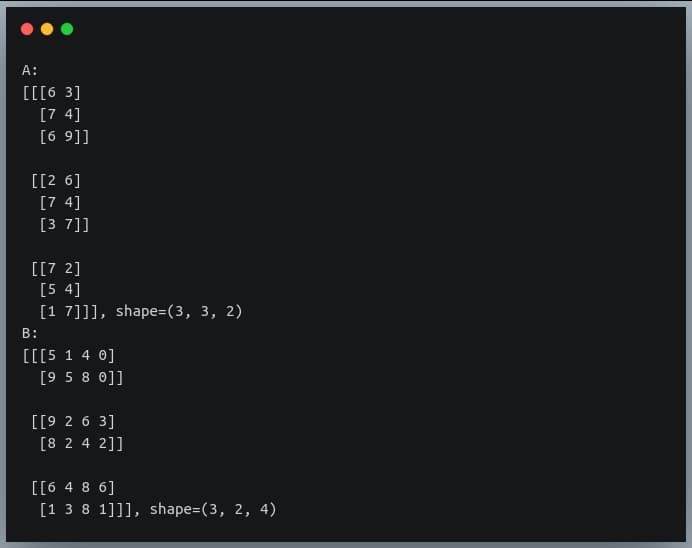
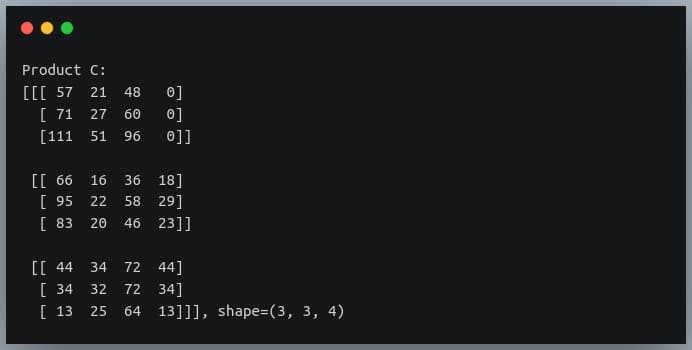
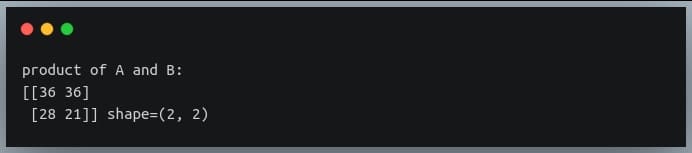
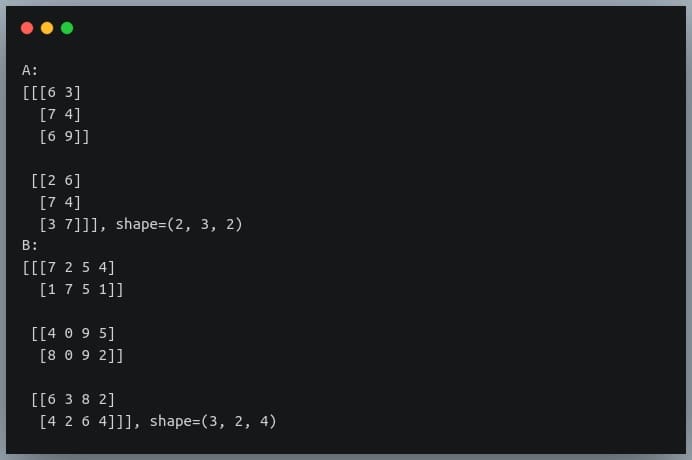
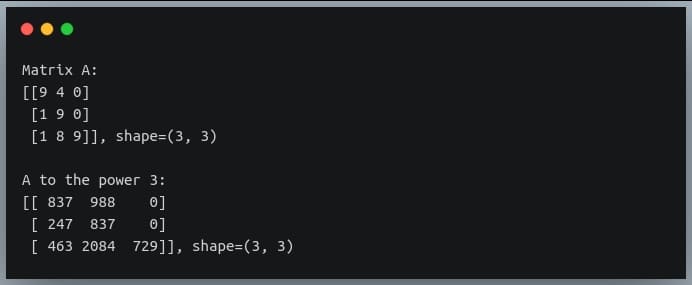
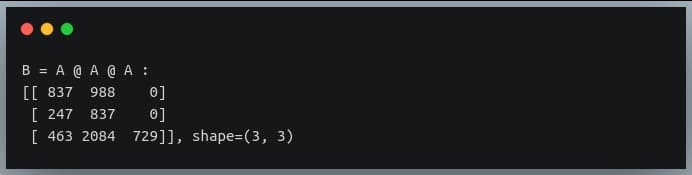
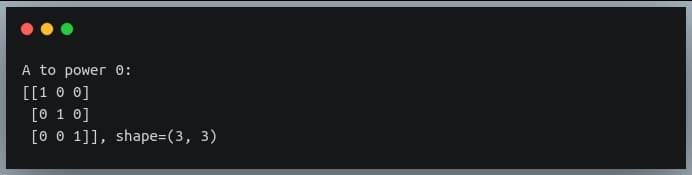
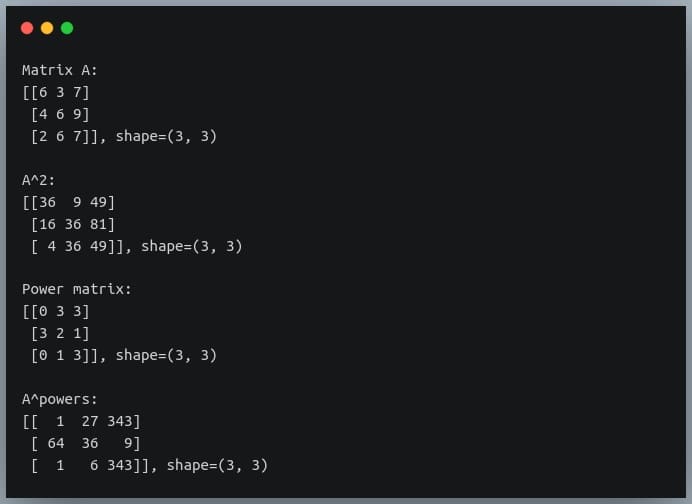
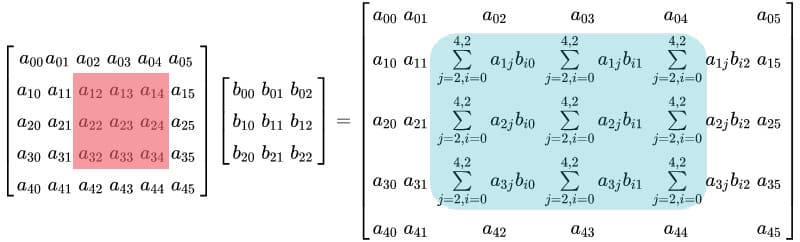
 In this tutorial, we will look at various ways of performing matrix multiplication using
In this tutorial, we will look at various ways of performing matrix multiplication using 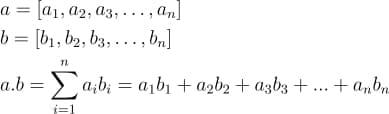
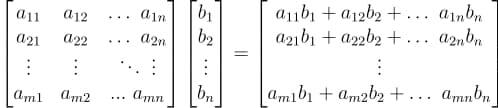
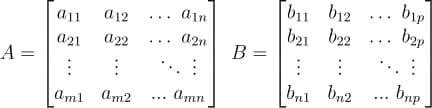

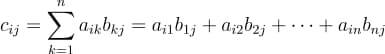
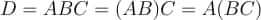
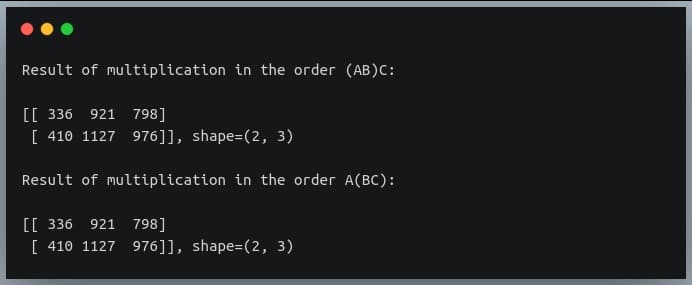
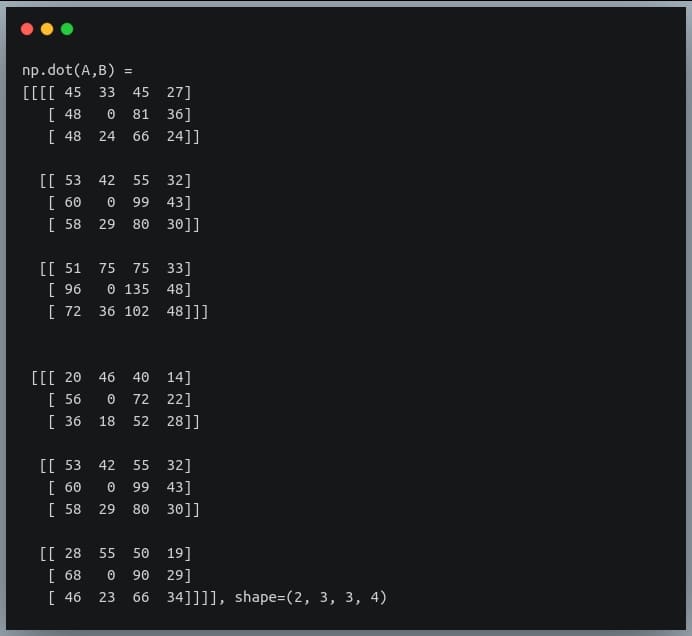
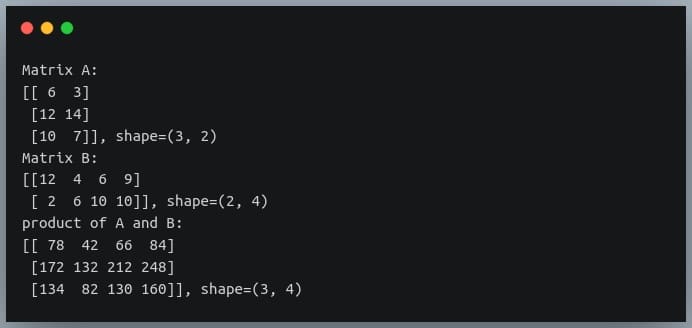
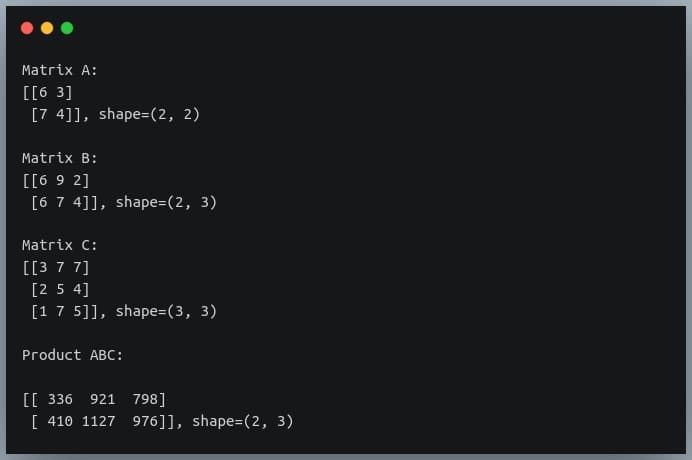
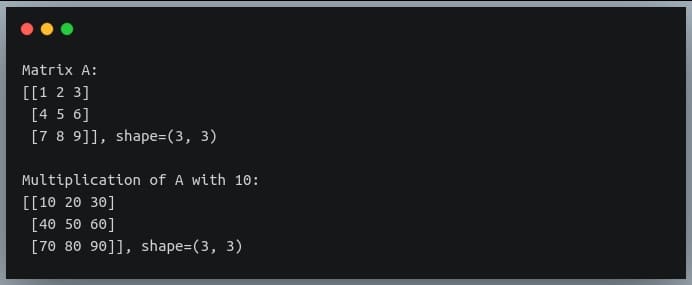
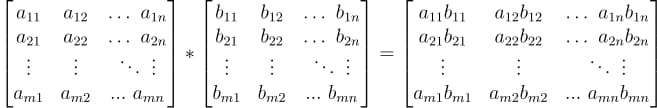
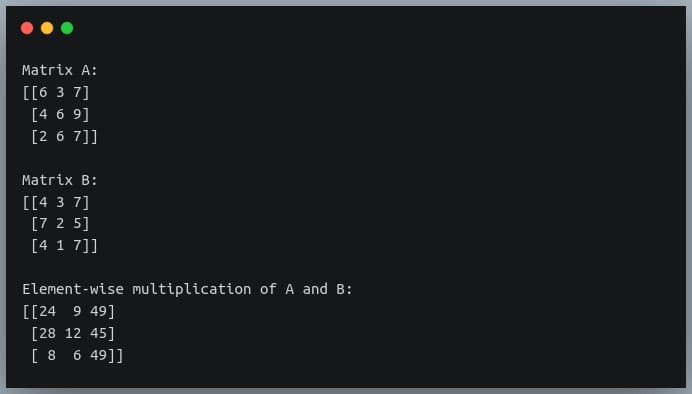
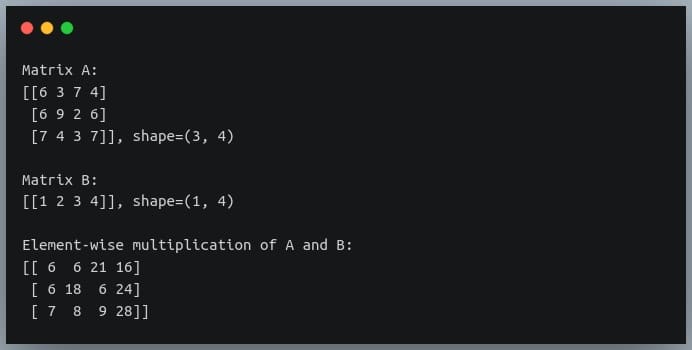
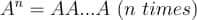
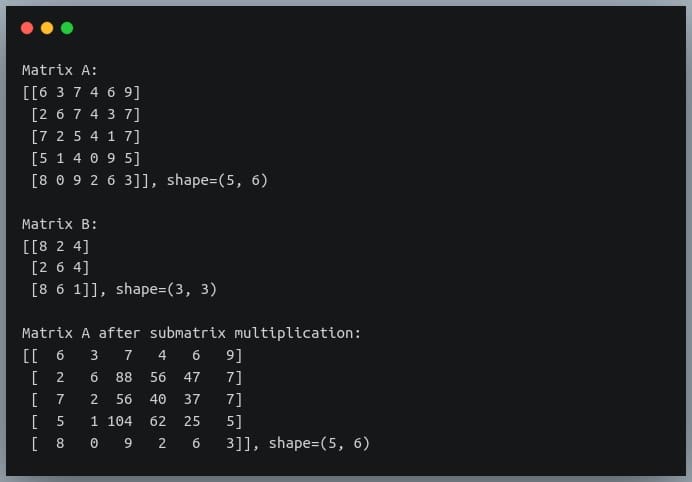


 In a previous tutorial, we talked about NumPy arrays and we saw how it makes the process of reading, parsing and performing
In a previous tutorial, we talked about NumPy arrays and we saw how it makes the process of reading, parsing and performing 




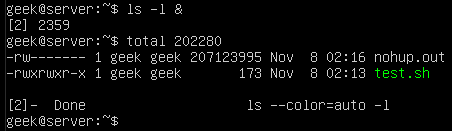

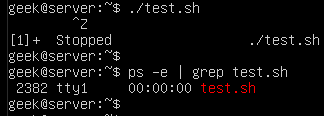
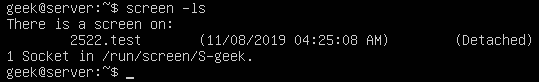
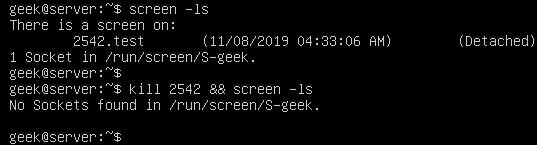
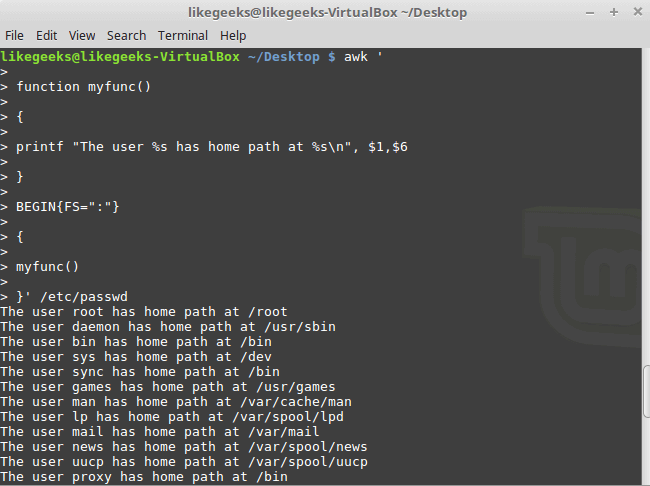
 If you want to process large files using PHP, you may use some of the ordinary PHP functions like file_get_contents() or file() which has a limitation when working with very large files. These functions rely on the memory_limit setting in php.ini file, you may increase the value but these functions still are not suitable for very large files because these functions will put the entire file content into memory at one point. Any file that has a size larger than memory_limit setting will not be loaded into memory, so what if you have 20 GB file and you want to process it using PHP? Another limitation is the speed of producing output. Let’s assume that you will accumulate the output in an array then output it at once which gives a bad user experience. For this limitation, we can use the yield keyword to generate an immediate result.
If you want to process large files using PHP, you may use some of the ordinary PHP functions like file_get_contents() or file() which has a limitation when working with very large files. These functions rely on the memory_limit setting in php.ini file, you may increase the value but these functions still are not suitable for very large files because these functions will put the entire file content into memory at one point. Any file that has a size larger than memory_limit setting will not be loaded into memory, so what if you have 20 GB file and you want to process it using PHP? Another limitation is the speed of producing output. Let’s assume that you will accumulate the output in an array then output it at once which gives a bad user experience. For this limitation, we can use the yield keyword to generate an immediate result. In the previous post, we talked about
In the previous post, we talked about